propiedades de los logaritmos

El logaritmo en base 

$b$$b$
del número positivo $a$$a$ se denota por $l$$o$$g^{}$${}_b$$($$a$$)$$lo{g}_b(a)$ y su valor es el número $c$$c$ al que se debe elevar la base del logaritmo, $b$$b$, para obtener el número $a$$a$. Es decir,

logb(a)=c⇔bc=a Ejemplos:

• el logaritmo en base 2 de 8 es 3 porque 2 al cubo es 8:
  
  
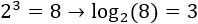
• el logaritmo en base 10 de 100 es 2 ya que 10 al cuadrado es 100:
  
  
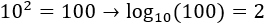
• el logaritmo en base $e$ (logaritmo natural, $lo{g}_e=ln$) de $e^3$es 3 ya que $e$ al cubo es $e^3$:
  
  

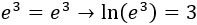
Las siguientes propiedades son

Logaritmo del producto:

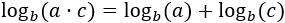Logaritmo del cociente:

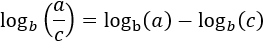*Logaritmo de la potencia:

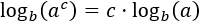Cambio de base:

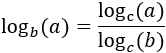Propiedad útil en la práctica:

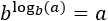Cambio de base

aquella en la que la incógnita aparece, únicamente, en los exponentes de potencias de bases constantes.¹​ La incógnita puede aparecer en el exponente de uno o más términos, en cualquier miembro de la ecuación. Es decir, una constante está elevada a una función de la incógnita a despejar, usualmente representada por x. Para resolver dichas ecuaciones se recurren a las propiedades de la potenciación, la radicación, de los logaritmos y cambio de la incógnita por otra.

Sea la ecuación del siguiente ejemplo:

${\displaystyle 2^{x+1}=16\,}$

Si el primer miembro sólo tiene un término y el término del segundo miembro es potencia de la base del término del primer miembro, entonces el segundo miembro, se expresa como potencia de la base de la expresión que contiene la incógnita. En el ejemplo 16 es potencia de la base dos de ${\displaystyle 2^{x+1}}$.

${\displaystyle 2^{x+1}=2^{4}\,}$

Luego, por la siguiente propiedad: ${\displaystyle a^{x}=a^{y}\Rightarrow x=y\,}$, tenemos: ${\displaystyle x+1=4\,}$

${\displaystyle x=4-1\,}$

${\displaystyle x=3\,}$

• Un ejemplo algo variado

4^2x-1 = 2^x

Puesto que 4 = 2² en la ecuación dada resulta

2^2(2x-1) = 2^x

Finamente, resolviendo 2(2x-1) = x, se obtiene x = 2/3.

Cambio de variables

Artículo principal: Cambio de variable

Sea la ecuación exponencial del ejemplo:

${\displaystyle 2\cdot 7^{x+2}+7^{x}=33957\,}$

Vamos a escribirla así:

${\displaystyle 2\cdot (7^{x})\cdot 7^{2}+(7^{x})=33957}$

Aplicamos el cambio de variable, y escribimos:

${\displaystyle 7^{x}=a\,}$

Ahora, al reemplazar, se tiene:

${\displaystyle 2a\cdot 49+a=33957\,}$

Despejamos ${\displaystyle a\,}$:

${\displaystyle 99a=33957\,}$

${\displaystyle a={\frac {33957}{99}}\,}$

${\displaystyle a=343\,}$

Ahora, recordemos que ${\displaystyle a=7^{x}\,}$, luego:

${\displaystyle 343=7^{x}\,}$

${\displaystyle 7^{3}=7^{x}\,}$

${\displaystyle 3=x\,}$

Pasando a una algebraica

Resolver la ecuación³​

2·9^2x - 3^x+1 -2 = 0

Puesto que la ecuación propuesta puede ser escrita en la forma

2·(3^x)² - 3·3^x - 2 = 0

Luego con la sustitución y = 3^x, se tiene respecto a y la ecuación algebraica de segundo grado

2y² - 3y -2 = 0.

Resolviendo resulta y = 2; y = -1/2. La última solución es imposible, pues 3^x > 0. En tal caso 3^x = 2;

x = log₃2 = ln2 : ln3 = 0.6309 ( logaritmos naturales);

Usando logaritmos

Artículo principal: Logaritmo binario

Sea la ecuación:

${\displaystyle 4^{x+1}\cdot 8^{x}=4096\,}$

Usamos logaritmo a ambos lados de la ecuación:

${\displaystyle \log _{2}(4^{x+1}\cdot 8^{x})=\log _{2}4096}$

Por propiedades de los logaritmos, tenemos:

${\displaystyle \log _{2}(4^{x+1})+\log _{2}(8^{x})=\log _{2}4096}$

${\displaystyle (x+1)\cdot \log _{2}4+x\cdot \log _{2}8=\log _{2}4096\,}$

Operando:

${\displaystyle (x+1)\cdot 2+x\cdot 3=12\,}$

${\displaystyle 2x+2+3x=12\,}$

${\displaystyle 5x=10\,}$

De donde sale:

${\displaystyle x=2\,}$