Revisar
En primer lugar, comenzar con las propiedades de la gráfica de la función exponencial de base de una base,
f (x) = ax , a > 0 y no es igual a 1.
El dominio de la función f es el conjunto de todos los números reales. El rango de f es el intervalo (0, + infinito).
La gráfica de f tiene una asíntota horizontal dada por y = 0. Función f tiene interceptar ay en (0, 1). f es una función creciente si a es mayor que 1 y una función decreciente si a es menor que 1.
Es posible que desee revisar todas las propiedades anteriormente mencionadas de la función exponencial de forma interactiva.
Ejemplo 1: f es una función dada por
f (x) = 2 (x - 2)
- Encuentra el dominio y el rango de f.
- Encuentra la asíntota horizontal de la gráfica.
- Encuentra la X y la intercepta y de la gráfica. de f si los hay.
- Dibuje la gráfica de f.
Revisar
En primer lugar, comenzar con las propiedades de la gráfica de la función exponencial de base de una base,
f (x) = ax , a > 0 y no es igual a 1.
El dominio de la función f es el conjunto de todos los números reales. El rango de f es el intervalo (0, + infinito).
La gráfica de f tiene una asíntota horizontal dada por y = 0. Función f tiene interceptar ay en (0, 1). f es una función creciente si a es mayor que 1 y una función decreciente si a es menor que 1.
Es posible que desee revisar todas las propiedades anteriormente mencionadas de la función exponencial de forma interactiva.
Respuesta a la Ejemplo 1
- El dominio de f es el conjunto de todos los números reales. Para encontrar el rango de f, empezamos con
Multiplica ambos lados por 2 -2 lo cual es positivo.
Usar las propiedades exponencial
Esta última declaración sugiere que f (x)> 0. El rango de f es (0, + inf).
Como x disminuye sin límite, f (x) = 2 (x - 2) se aproxima a 0. La gráfica de f tiene una asíntota horizontal en y = 0.
Para encontrar la intersección x tenemos que resolver la ecuación
Esta ecuación no tiene solución, consulte el rango de lo anterior, f (x)> 0. La gráfica de f no tiene una x interceptar. La intersección está dada por(0, f (0)) = (0,2 (0 - 2)) = (0, 1 / 4).
Hasta el momento tenemos el dominio, rango, intersección y la asíntota horizontal. Necesitamos puntos extra.(4, f (4)) = (4, 2 (4 - 2)) = (4, 2 2) = (4, 4)
(-1, F (-2)) = (-1, 2 (-1 - 2)) = (-1, 2 -3) = (-1, 1 / 8)
graficar f.
Igualados Problema Ejemplo 1: f es una función dada por
f (x) = 2 (x + 2)
- Encuentra el dominio y el rango de f.
- Encuentra la asíntota horizontal de la gráfica de f.
- Encuentra la X y la intercepta y de la gráfica de f si los hay.
- Dibuje la gráfica de f.
Ejemplo 2: f es una función dada por
f (x) = 3 (x + 1) - 2
- Encuentra el dominio y el rango de f.
- Encuentra la asíntota horizontal de la gráfica de f.
- Encuentra la X y la intercepta y de la gráfica de f si los hay.
- Dibuje la gráfica de f.
Respuesta a la Ejemplo 2
- El dominio de f es el conjunto de todos los números reales. Para encontrar el rango de f, empezamos con
Multiplica ambos lados por 3, que es positivo.
Usar las propiedades exponencial
Resta 2 a ambos lados
Esta última declaración sugiere que f (x)> -2. El rango de f es (-2, + inf).
- Como x disminuye sin límite, f (x) = 3 (x + 1) -2 enfoques -2. La gráfica de f tiene una asíntota horizontal y = -2.
- Para encontrar la intersección x tenemos que resolver la ecuación f (x) = 0
Añadir de 2 a ambos lados de la ecuación de
Vuelva a escribir la ecuación anterior en forma logarítmica
Resuelva para x
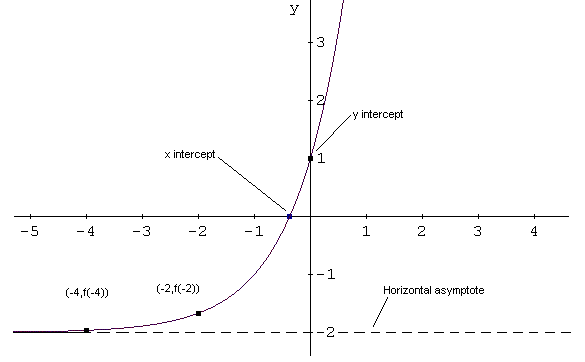
La intersección está dada por(0, f (0)) = (0,3 (0 + 1) - 2) = (0, 1).
- Hasta el momento tenemos el dominio, rango, x e intercepta y, y la asíntota horizontal. Necesitamos puntos extra.
(-2, F (-2)) = (-2, 3 (-2 + 1) - 2) = (4, 1/3-2) = (4, -1,67)
(-4, F (-4)) = (-4, 3 (-4 + 1) - 2) = (-4, 2 -3) = (-4, -1,99)
graficar f.
Igualados Problema Ejemplo 2: f es una función dada por
f (x) = 2 (x - 2) + 1
- Encuentra el dominio y el rango de f.
- Encuentra la asíntota horizontal de la gráfica de f.
- Encuentra la X y la intercepta y de la gráfica de f si los hay.
- Dibuje la gráfica de f.
|
|
|

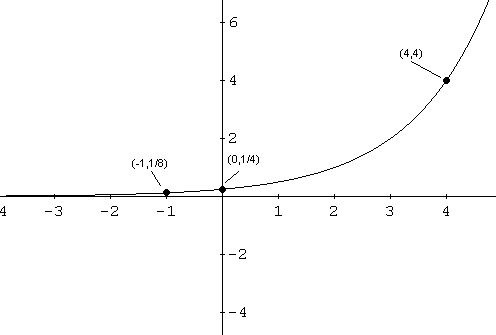
No hay comentarios.:
Publicar un comentario