Ecuaciones exponenciales

Es imprescindible conocer las propiedades de las potencias ya que nos permiten simplificar las ecuaciones. Generalmente, escribiremos los números enteros de las ecuaciones en su forma de potencia.

Ecuación básica

La ecuación por la que empezamos es una igualdad entre una exponencial y un número entero que puede escribirse como una potencia con la misma base que la exponencial.
Por ejemplo, la ecuación $5^x=125$
puede escribirse como
$$5^x=5^3$$
Teniendo en cuenta que dos potencias con la misma base son iguales si, y solamente si, sus exponentes son iguales, la solución de la ecuación $5^x=5^3$
es $x=3$.

Ecuación 1

Resolver la ecuación igualando exponentes de potencias con base común: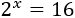

Solución

A veces, también tendremos que escribir las bases de las exponenciales como potencias. Por ejemplo, en la ecuación

escribimos 16 como la potencia $2^4$
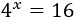
y la base de la exponencial $4^x$ como $4=2^2$ para tener bases comunes:

Si tenemos números, potencias o exponenciales que multiplican a las exponenciales, podemos simplificarlas aplicando las propiedades de las potencias.
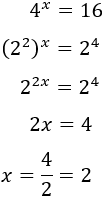
Por ejemplo,

• si tenemos $2\cdot 2^x$

, eliminamos el 2 de la izquierda escribiendo +1 en el exponente:

si tenemos $4\cdot 2^x$

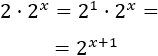
• , eliminamos el 4 de la izquierda escribiendo +2 en el exponente:
  
  

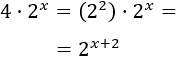
Ecuación 2

Resolver la ecuación escribiendo potencias cuyas bases sean iguales y números primos: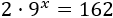

Ecuación 3

Resolver siguiendo los ejemplos anteriores: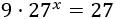

Cambio de variable

Cuando en los exponentes tenemos coeficientes en la incógnita, podemos aplicar un cambio de variable. Normalmente, será suficiente un cambio como $2^x=t$
ó $3^x=t$ (la base dependerá de las exponenciales de la ecuación).
Por ejemplo, para resolver la siguiente ecuación, aplicaremos el cambio de variable $2^x=t$
y obtendremos una ecuación de segundo grado:

Las soluciones de la ecuación de segundo grado son

Como $t=2^x$
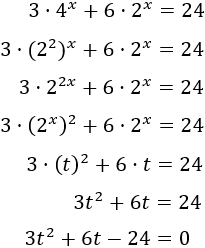
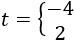
, tenemos

La primera ecuación, $2^x=-4$
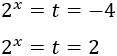
no tiene solución real (porque la potencia de un número positivo no puede ser negativo).
De la segunda ecuación ,tenemos que $x=1$
.

Ecuación 4

Resolver mediante el cambio de variable $t=3^x$

:

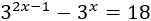
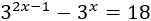
Ecuación 5

Resolver mediante el cambio de variable $t=7^{-x}$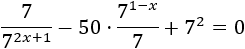

Ecuación exponencial con raíces

Como las raíces son potencias con fracciones en los exponentes, podemos encontrar ecuaciones exponenciales con signos radicales. Las resolveremos prácticamente del mismo modo.
Hay que recordar que

Por ejemplo, resolvemos la siguiente ecuación que tiene la incógnita en una raíz:

Escribimos la raíz y el número 16 como potencias:

Para resolver la ecuación anterior, pasamos $x-1$
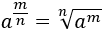
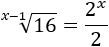
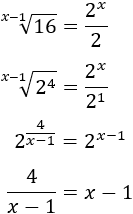
multiplicando al otro lado:

Resolvemos la ecuación de segundo grado:

La ecuación exponencial tiene dos soluciones: $x=3$
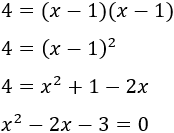
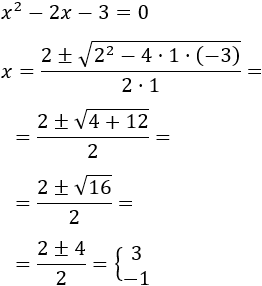
y $x=-1$.

Ecuación 6

Resolver escribiendo las raíces como potencias: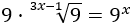

Soluciones logarítmicas

Si no tenemos potencias con la misma base, la solución de la ecuación suele ser un logaritmo. Para trabajar estas ecuaciones, tenemos que utilizar las propiedades de los logaritmos.
La definición del logaritmo de base $b$
es

En otras palabras, el logaritmo en base $b$
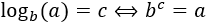
del número $a$ es el número al que hay que elevar $b$ para obtener $a$. Por ejemplo, el logaritmo en base 2 de 8 es 3 porque 2 elevado a 3 es 8:

La solución de la ecuación $3^x=5$
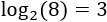
es el número al que hay que elevar 3 para obtener 5, es decir, es precisamente el logaritmo en base 3 de 8 (aplicar logaritmos en ambos lados de la igualdad):

Otra forma de entender lo anterior es:
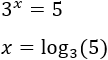
Como $3^x$
debe ser igual a 5, entonces el logaritmo en base 3 de $x$ debe ser igual al logaritmo en base 3 de 5:

El último paso se debe a la definición del logaritmo: el logaritmo en base 3 de $3^x$
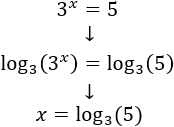
es el número al que hay que elevar 3 para obtener $3^x$.

Ecuación 7

Resolver mediante logaritmos en base 2: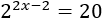

Solución

También, podemos escoger un logaritmo en base distinta a las bases de las exponenciales. Por ejemplo, aplicamos logaritmo en base 10 para resolver la siguiente ecuación:

En adelante, si no escribimos la base de un logaritmo es porque ésta es 10.

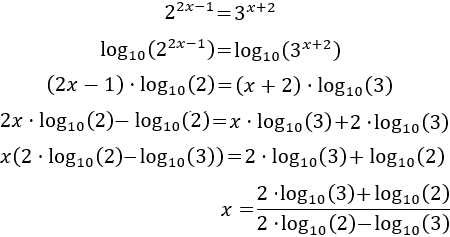
Ecuación 8

Resolver la ecuación exponencial siguiente aplicando un cambio de variable (primero) y logaritmos en base 2 (después):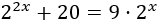

Ecuación 9

Resolver mediante logaritmos en base 5: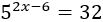

https://www.youtube.com/watch?v=v-ywxicyECU