Gráfica de las funciones trigonométricas.
Definición de círculo trigonométrico
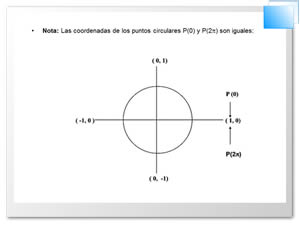
El círculo unitario es un círculo de radio 1 con centro en el origen del sistema de coordenadas, esto es, el punto (0,0)
Cada número real de la recta numérica se asocia
con las coordenadas de un punto en el círculo unitario llamado punto
circular. Para eso, luego, localizamos el 0 en la recta numérica de
manera que coincida con el punto (1, 0) en la unidad del círculo.
Como el radio del círculo unitario es 1, entonces la
circunferencia del círculo es, entonces, el eje real positivo se
enrolla en sentido contrario a las manecillas del reloj y el eje real
negativo se enrolla en el sentido de las manecillas del reloj. De
manera, que cada número real de la recta real se asocia con un sólo
punto circular del círculo unitario.
Funciones de ángulos de cualquier magnitud
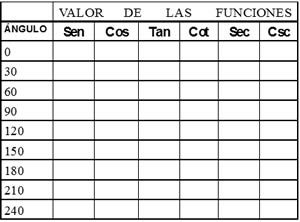
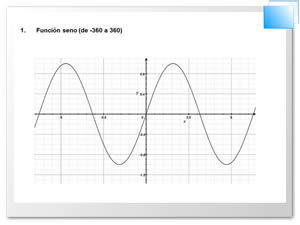
Variación y gráficas de las funciones trigonométricas (seno, coseno, tangente, cotangente, secante y cosecante)
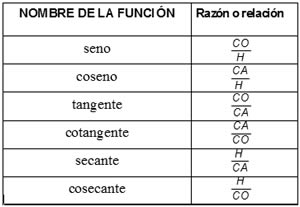
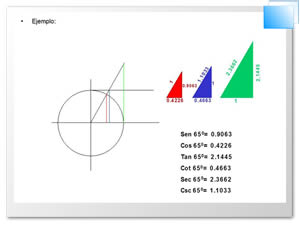
Las funciones trigonométricas de un triángulo rectángulo son las razones o relaciones entre sus lados.
Las funciones trigonométricas son algunas aplicaciones que nos ayudan en la resolución de triángulos rectángulos Un triángulo tiene seis elementos: tres lados y tres ángulos. Resolver un triángulo consiste en calcular tres de los elementos cuando se conocen los otros tres, siempre que uno de ellos sea un lado.
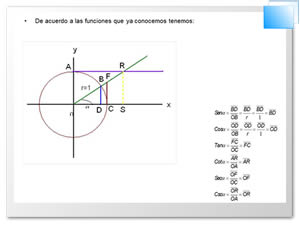
Gráficas de las funciones trigonométricas
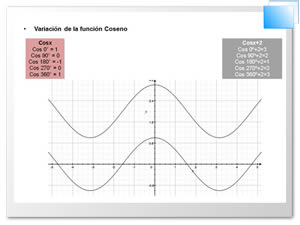
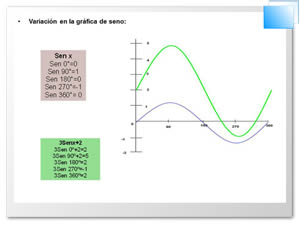
Si queremos representar en forma gráfica una
función trigonométrica tomamos los valores de la variable independiente
como abscisas y los valores de la función como ordenadas, obteniendo
así una serie de puntos, los que al unirlos nos dará una línea que será
la representación gráfica de la función.
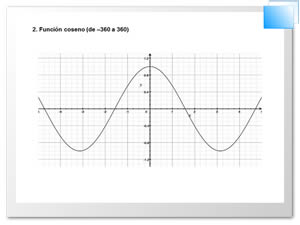
Uso de la función seno: ésta se usa cuando en un
triángulo rectángulo se conoce un ángulo agudo y el cateto opuesto, o un
ángulo agudo y la hipotenusa, o el cateto opuesto al ángulo dado. Uso de la función coseno: si en un triángulo rectángulo conocemos un ángulo agudo y el cateto adyacente, o un ángulo agudo y la hipotenusa.
Podemos calcular el cateto adyacente al ángulo dado y la hipotenusa usando esta función.
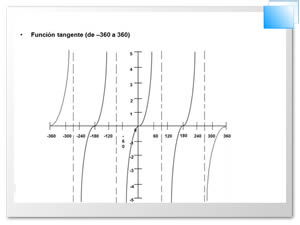
Uso de la función tangente: si en un triángulo rectángulo conocemos un cateto y el ángulo adyacente a él podemos calcular el otro cateto.
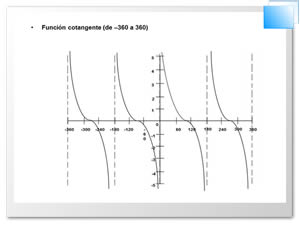
Uso de la función cotangente: por lo tanto en todo triángulo rectángulo si conocemos un cateto y su ángulo opuesto podemos calcular el valor del otro mediante ésta.
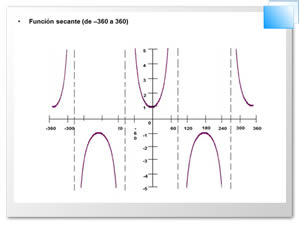
Uso de la función secante: ésta se usa cuando se tiene lo contrario que en la función coseno.
Uso de la función cosecante: ésta se usa cuando se tiene lo contrario a la función seno.
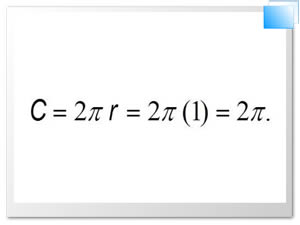

No hay comentarios.:
Publicar un comentario